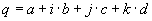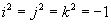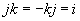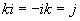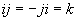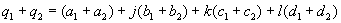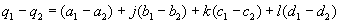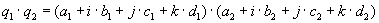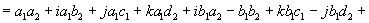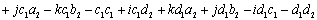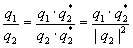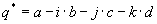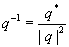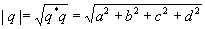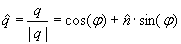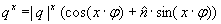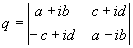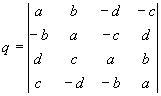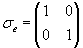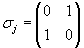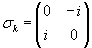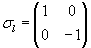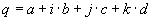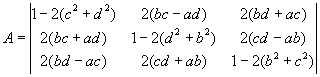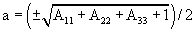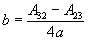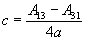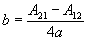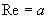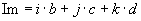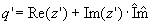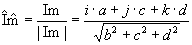Quaternionen
|
Quaternionen sind komplexen Zahlen und hyperkomplexen Zahlen ähnlich. Allerdings ist die Multiplikation nicht kommutativ (vertauschbar)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Formulierung einer räumlichen Drehung
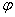 entspricht dem Winkel um den gedreht wird. entspricht dem Winkel um den gedreht wird.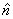 entspricht der Achse um die gedreht wird. entspricht der Achse um die gedreht wird.Anwendung finden die Quaternionen heute hauptsächlich in der Computergraphik, da sich mit Ihnen Drehungen im Raum darstellen lassen. Außerdem werden sie noch in der Quantenmechanik bei der Beschreibung von Spins verwendet.
|
Rotationen mit Quaternionen
|
Ein Punkt P=(x,y,z) wird durch das Quaternion p = ix + jy + kz repräsentiert. Eine Rotation um die x-Achse um einen Winkel 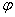 durch das Quaternion durch das Quaternion 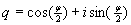 repräsentiert. repräsentiert.Der rotierte Punkt ist 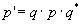 . .
|
Umwandlung von Quaternion in Rotationsmatrix
|
|
--> |
|
Umwandlung von Rotationsmatrix in Quaternion
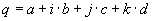 |
|
|
|
|
d |
Trigonometrische Funktionen von Quaternionen
|
Bei dem folgenden Lösungsverfahren werden aus den Quaternionen erst komplexe Zahlen erzeugt. Auf diese wird dann die Funktion im Komplexen angewendet. Danach wird das komplexe Ergebnis unter Berücksichtigung des ursprünglichen Quaternions wieder in ein Quaternion umgewandelt. Da es zu diesem Thema sehr wenige Veröffentlichungen gibt, weiss ich nicht genau, ob dies korrekt ist und ob es auf alle unten aufgeführten Funktionen anwendbar ist. Für Hinweise hierzu wäre ich dankbar. (email: calc_3d@greuer.de) |
Verfahren
Auf das Quaternion 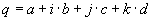 soll die Funktion func(q) angewendet werden. soll die Funktion func(q) angewendet werden.q lässt sich aufteilen in den |
|
Realteil |
|
und den |
Imaginärteil |
|
Daraus wird eine komplexe Zahl 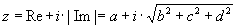 erzeugt. erzeugt.Auf diese komplexe Zahl wird die Funktion func(z) angewendet: 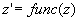 Unter Berücksichtigung des Imaginärteils des ursprünglichen Quaternions wird das Ergebnis erzeugt: |
|
|
mit |
|
|
Dieses Verfahren wird in Calc 3D auf folgende Funktionen angewendet: sin; cos; tan; sinh; cosh; tanh; arcsin; arccos; arctan; arccot; arsinh; arcosh; artanh; arcoth; log; exp |
| Zurück Weiter |
| Hilfe |
| Matrizen |
| Vektoren |
| Koordinaten |
| Komplexe Zahlen |
| Quaternionen |
| Häufige Fragen |
| Übersicht | Beschreibung | Bilder der Oberfläche | Download | Hilfe | Online Hilfe | Online Rechner | Kontakt | Bücher |
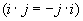 .Sie haben 3 Imaginärteile, die im folgenden mit den Buchstaben j, k und l markiert werden. Der Realteil hat bei dieser Schreibweise keine Markierung.
.Sie haben 3 Imaginärteile, die im folgenden mit den Buchstaben j, k und l markiert werden. Der Realteil hat bei dieser Schreibweise keine Markierung.