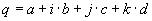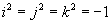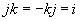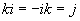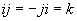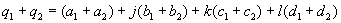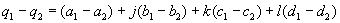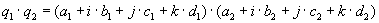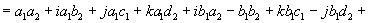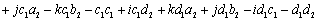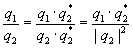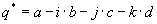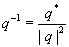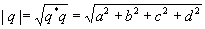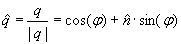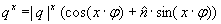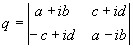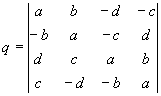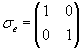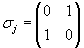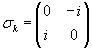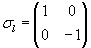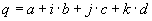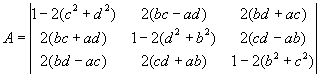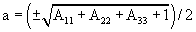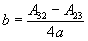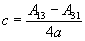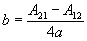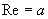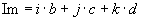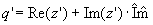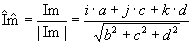Quaterniones
|
Quaternions are similar to complex and hyper complex numbers, but their multiplication is not cummutative
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Description of rotation
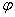 corresponds to the rotation angle. corresponds to the rotation angle.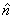 corresponds to the rotation axis. corresponds to the rotation axis.Quaternions are mainly used in computer graphics to descibe rotations in the space. Also they are used in quant mechanics to describe spins. Doing this, put instead of the marks (e,i,j,k) the Pauli spin matrices:
|
Rotations with quaternions
|
A point P=(x,y,z) is represented with the quaternion p = ix + jy + kz . A rotation of the angle 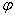 around the x-axis is represented with the quaternion around the x-axis is represented with the quaternion 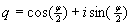 . .
The rotated point is 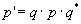 . .
|
Conversion of quaternion to rotation matrix
|
|
--> |
|
Conversion of rotation matrix to quaternion
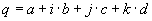 |
|
|
|
|
d |
Trigonometric functions of quaternions
|
At the following procedure in a 1st step the quaternions will be converted to complex numbers. Then in a 2nd step the complex funktion is executed. In a 3rd step the complex result will be converted to a quaternion using the old quaternion. Because I didnot find a publication with a proper description about this topic, I don’t know whether this is correct and whether I can use this procedure for all function I used it. It would be nice to get a hint about this. (email: calc_3d@greuer.de) |
Procedure
With the quaternion 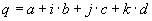 The function func(q) should be executed The function func(q) should be executedq can be seperated into the |
|
real part |
|
und den |
imaginary part |
|
With this a complex number 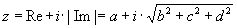 is created. is created.The function func(z) is executed with this complex number: 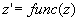 Using the imaginary part of the former quaternion the result is created: |
|
|
with |
|
|
This procedure is used in Calc 3D for the following functions: sin; cos; tan; sinh; cosh; tanh; arcsin; arccos; arctan; arccot; arsinh; arcosh; artanh; arcoth; log; exp |
| para diante em seguida |
| Ajuda |
| Matrices |
| Vetor |
| Coordenadas |
| Números complexos |
| Quaterniones |
| FAQ |
| Vista geral | Características | Screenshots | Download | Ajuda | Online ajuda | Online calculators | Contato |
 They have 3 non real parts, that are marked here with the letters j, k and l. The real part will not have an own letter here.
They have 3 non real parts, that are marked here with the letters j, k and l. The real part will not have an own letter here.